[学习目标]

1.理解三角形内角和定理的证明方法;

2.掌握三角形内角和定理及三角形的外角性质;

3.能够运用三角形内角和定理及三角形的外角性质进行相关的计算，证明问题.

[要点梳理]

要点一、三角形的内角

1.三角形内角和定理:三角形的内角和为 180°.

要点诠释:应用三角形内角和定理可以解决以下三类问题:

① 在三角形中已知任意两个角的度数可以求出第三个角的度数；

② 己知三角形三个内角的关系，可以求出其内角的度数；

③ 求一个三角形中各角之间的关系.

2.直角三角形:如果一个三角形是直角三角形，那么这个三角形有两个角互余。反过来，有两个角互余的三角形是直角三角形。

要点诠释:

如果直角三角形中有一个锐角为45°,那么这个直角三角形的另一个锐角也是45°，且此直角 三角形是等腰直角三角形。

要点二、三角形的外角

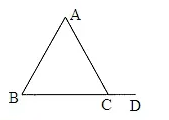
1.定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角如图，∠ACD是△ABC的一个外角

要点诠释:

(1) 外角的特征:

① 顶点在三角形的一个顶点上:

② 一条边是三角形的一边:

③ 另一条边是三角形某条边的延长线.

(2) 三角形每个顶点处有两个外角，它们是对顶角。所以三角形共有六个外角，通常每个顶 点处取一个外角，因此，我们常说三角形有三个外角。

2.性质:

(1) 三角形的一个外角等于与它不相邻的两个内角的和

(2) 三角形的一个外角大于任意一个与它不相邻的内角要点诠释:三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据。另外，在证角的不等关系时也常想到外角的性质。

3.三角形的外角和:三角形的外角和等于360°

要点诠释:

因为三角形的每个外角与它相邻的内角是邻补角，由三角形的内角和是180°, 可推出三角形的三个外角和是360°.